あなたは、どのコース（検波回路）を選びますか？（１）とにかく簡易型スペアナとして安価に製作したい人
---->ダイオード検波回路
（２）簡易型ではあるが、そこそこ性能のあるスペアナとして製作したい人
---->反転型・半波整流検波回路
（３）本格的にスペアナを製作したく、性能面を重視したい人
---->全波整流検波回路
これまで解説してきた整流回路ですが、大きく分けて半波整流と全波整流回路があります。半波整流回路では、非反転型と反転型に分けられます。各種ある中で、スペアナの検波回路として使っていくためには、どの回路が一番良いか検討しましょう。
あなたは、どのコース（検波回路）を選びますか？
（１）とにかく簡易型スペアナとして安価に製作したい人
---->ダイオード検波回路
（２）簡易型ではあるが、そこそこ性能のあるスペアナとして製作したい人
---->反転型・半波整流検波回路
（３）本格的にスペアナを製作したく、性能面を重視したい人
---->全波整流検波回路
ダイオード検波回路
とにかく簡易型スペアナとして安価に製作したい人は、図１の回路のように、ダイオードＤ（順方向電圧の小さいゲルマニウム・ダイオードや、ショットキ・バリア型）を使用して半波整流します。この回路は、ダイオードの順方向電圧の影響を受けるため、入力電圧の振幅が小さいと誤差が大きくなります。検波出力をＡＤ変換し、ソフトで出力値を補正する必要がありますが、数１００ＭＨｚ程度までの周波数も検波することが可能で、なんと言っても簡単なのがこの回路です。
 |
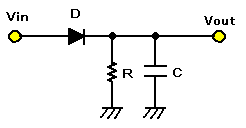| 図１．ダイオード検波回路例 |
反転型・半波整流検波回路
簡易型ではあるが、そこそこ性能のあるスペアナとして製作したい人にお勧めです。４５５ｋＨｚで歪を少なくするには、ＬＭ６３６１などの高速ＯＰアンプが必要になってきます。図２に反転型・半波整流検波回路の例を示します。
 |
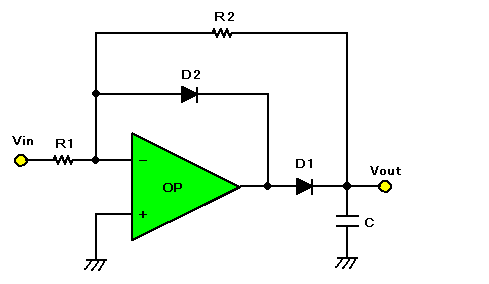| 図２．反転型・半波整流検波回路 |
検波回路の負荷抵抗Ｒ（RはＲ２に相当）と平滑コンデンサＣの値ですが、時定数τ＝ＣＲによって出力波形がどのように変化するか次に見てみましょう。使用したパーツは、ＯＰアンプＬＭ６３６１を用いて電源電圧±１２Ｖで動作させました。また、ダイオードＤ１，Ｄ２は１Ｎ６０を接続し、抵抗には一般の炭素皮膜抵抗で、Ｒ１＝Ｒ２＝１０ｋΩを接続しました。ここで、負荷抵抗はＲ（＝Ｒ２）＝１０ｋΩとなります。平滑用コンデンサは、Ｃ＝０ｐＦ（無接続）、１００ｐＦ、１０００ｐＦを、それぞれ付けた場合でデータを取りました。入力周波数は、ｆ＝４５５ｋＨｚです。
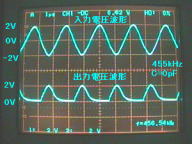図３（ａ）．反転型・半波整流検波回路
Ｃ＝０ｐＦ（無接続）のときの
入力／出力波形
上段：入力波形（４５５ｋＨｚ正弦波）
下段：出力波形（半波整流検波出力）
（縦軸：２Ｖ／ｄｉｖ，横軸：１μｓ／ｄｉｖ）
図３（ａ）は、Ｃ＝０ｐＦ（無接続）のときです。出力電圧波形のピークの形状ですが、やや右側がなだらかに見えます。これは、基板の配線容量や、オシロスコープのプローブの容量が影響しているためと思われます。
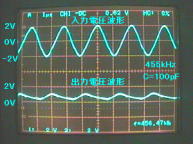図３（ｂ）．反転型・半波整流検波回路
Ｃ＝１００ｐＦ接続のときの
入力／出力波形
上段：入力波形（４５５ｋＨｚ正弦波）
下段：出力波形（半波整流検波出力）
（縦軸：２Ｖ／ｄｉｖ，横軸：１μｓ／ｄｉｖ）
図３（ｂ）は、Ｃ＝１００ｐＦを接続したものです。出力電圧波形のピークの形状がなだらかになり、波打っているように見えます（リップルという）。検波回路としては、まだ不十分ですので、もう少し容量を大きくする必要があります。時定数は、τ＝ＣＲ＝１[μｓ]です。
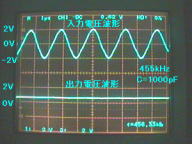図３（ｃ）．反転型・半波整流検波回路
Ｃ＝１０００ｐＦ接続のときの
入力／出力波形
上段：入力波形（４５５ｋＨｚ正弦波）
下段：出力波形（半波整流検波出力）
（縦軸：２Ｖ／ｄｉｖ，横軸：１μｓ／ｄｉｖ）
図３（ｃ）は、Ｃ＝１０００ｐＦを接続したものです。出力電圧波形のリップルが無くなり、検波回路として十分使用できる段階になりました。時定数は、τ＝ＣＲ＝１０[μｓ]です。
全波整流検波回路
本格的にスペアナを製作したく、性能面を重視したい人にお勧めです。４５５ｋＨｚで歪を少なくするには、ＬＭ６３６１などの高速ＯＰアンプが必要になってくることと、精度を向上させるために高精度抵抗が必要になってきます。
図４に全波整流検波回路の例を示します。全波整流回路の解説ページで紹介したＲ３の経路ですが、時間遅れ要素は特に考慮しませんでした。スペアナの検波回路として、絶対値出力を平均化して直流化する場合はあまり問題とはなりません。
さて、ここでノウハウを一つご紹介します。平滑回路のコンデンサの接続ですが、ＣをＯＰ２の出力と反転端子間に接続しています。ＯＰ２は、いわゆる積分回路となり、ローパスフィルタの役目を果たします。時定数はτ＝Ｒ５・Ｃとなります。ＯＰ２アンプの出力インピ−ダンスが低いため、反転型・半波整流回路のようにＣを出力端子とＧＮＤ間に直接入れることはできません。もし、入れるとしたら、負荷抵抗Ｒを介してから接続するようにします。この例ではＲ５を負荷抵抗Ｒとみなすことで、１本でも抵抗の本数を削減しています。
 |
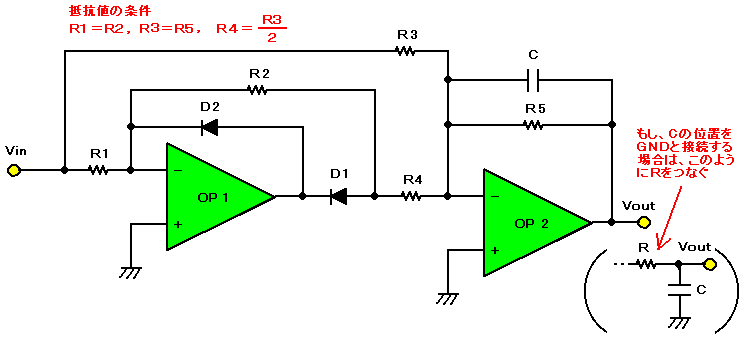| 図４．全波整流検波回路 |
全波整流回路の抵抗は、金属被膜抵抗など高精度のものを必要とします。ここは迷わず集合抵抗を使います。集合抵抗は部品点数を減らすだけでなく、全波整流回路のように抵抗比が重要な回路に効果的です。例えば１０ｋΩの集合抵抗では、Ｒ１＝Ｒ２＝Ｒ３＝Ｒ５＝１０ｋΩ、Ｒ４は１０ｋΩ抵抗×２個を並列接続して５ｋΩとします。図５の集合抵抗では４個の抵抗で構成されていますので、Ｒ１、Ｒ２の組合わせで１個使用し、Ｒ３、Ｒ５、Ｒ４のパラ接続の組合わせで集合抵抗を使うことになるでしょう。
図５．集合抵抗の外観
抵抗値は１０ｋΩ
４個入り
検波回路の時定数τ＝ＣＲによって出力波形がどのように変化するか次に見てみましょう。使用したパーツは、ＯＰアンプＬＭ６３６１を２個用いて電源電圧±１２Ｖで動作させました。また、ダイオードＤ１，Ｄ２は１Ｎ６０を接続し、抵抗には先程述べた１０ｋΩ集合抵抗を接続しました。ここで、負荷抵抗はＲ（＝Ｒ５）＝１０ｋΩとなります。平滑用コンデンサは、Ｃ＝０ｐＦ（無接続）、１００ｐＦ、１０００ｐＦを、それぞれ付けた場合でデータを取りました。入力周波数は、ｆ＝４５５ｋＨｚです。
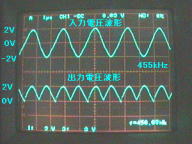図６（ａ）．全波整流検波回路
Ｃ＝０ｐＦ（無接続）のときの
入力／出力波形
上段：入力波形（４５５ｋＨｚ正弦波）
下段：出力波形（全波整流検波出力）
（縦軸：２Ｖ／ｄｉｖ，横軸：１μｓ／ｄｉｖ）
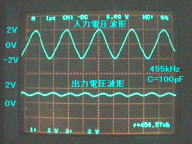図６（ｂ）．全波整流検波回路
Ｃ＝１００ｐＦ接続のときの
入力／出力波形
上段：入力波形（４５５ｋＨｚ正弦波）
下段：出力波形（全波整流検波出力）
（縦軸：２Ｖ／ｄｉｖ，横軸：１μｓ／ｄｉｖ）
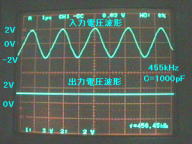図６（ｃ）．全波整流検波回路
Ｃ＝１０００ｐＦ接続のときの
入力／出力波形
上段：入力波形（４５５ｋＨｚ正弦波）
下段：出力波形（全波整流検波出力）
（縦軸：２Ｖ／ｄｉｖ，横軸：１μｓ／ｄｉｖ）
図６（ｃ）は、Ｃ＝１０００ｐＦを接続したものです。出力電圧波形のリップルが無くなり、検波回路として十分使用できる段階になりました。時定数は、τ＝ＣＲ＝１０[μｓ]です。
時定数τ＝ＣＲについて
ダイオード検波回路の負荷抵抗Ｒと平滑コンデンサＣの値ですが、時定数τ＝ＣＲを大きくすると検波効率を上げることができます。ただし、あまり過大になりすぎると、放電に要する時定数が長くなってしまいます。そうすると掃引したときに、スペアナの信号ピーク波形に検波包絡線が追いつかなくなって歪を発生します。これをダイヤゴナル・クリッピング歪と呼んでいます。
図７は、検波回路の入出力特性を示したものです。入力Ｖｉｎですが、中間周波数ｆ＝４５５ｋＨｚで、掃引により変調された山型のスペアナ・ピーク波形になっています。理想的には、Ｖｉｎの包絡線に沿って検波されるのがよいのですが、時定数τ＝ＣＲが過大すぎると検波出力は赤色の線で示したように歪みます。
 |
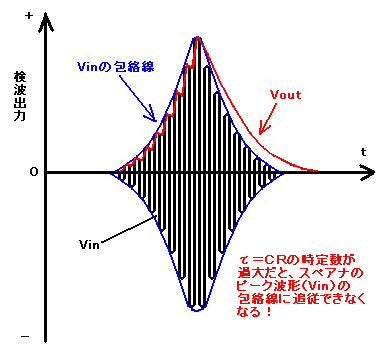| 図７．検波回路の入出力特性 |
この歪を改善するためには、
となる式を満足するような、Ｃ，Ｒを使用しなければなりません。ここで、ｆｍは掃引周波数に関係してきます。掃引周波数を速くするとＣＲの値を小さくしなくてはならず、検波効率は低下します。逆に、ＣＲを大きくして検波効率を上げることを優先すれば、掃引周波数を遅くする必要があります。実験結果では、Ｒ＝１０ｋΩ、Ｃ＝１０００ｐＦ程度の容量で（τ＝１０[μｓ]）、リップルは無視できるようです。
 |
|
 |